平滑化ラインプロット

折れ線グラフでは、平滑化（smoothing）を使用して、ノイズの多い データ の中からトレンドを確認できます。

W&B はいくつかの種類のスムージングをサポートしています：

• Time weighted exponential moving average (TWEMA) スムージング
• Gaussian スムージング
• Running average
• Exponential moving average (EMA) スムージング

これらが実際に動作している様子は、インタラクティブな W&B レポート で確認できます。

​

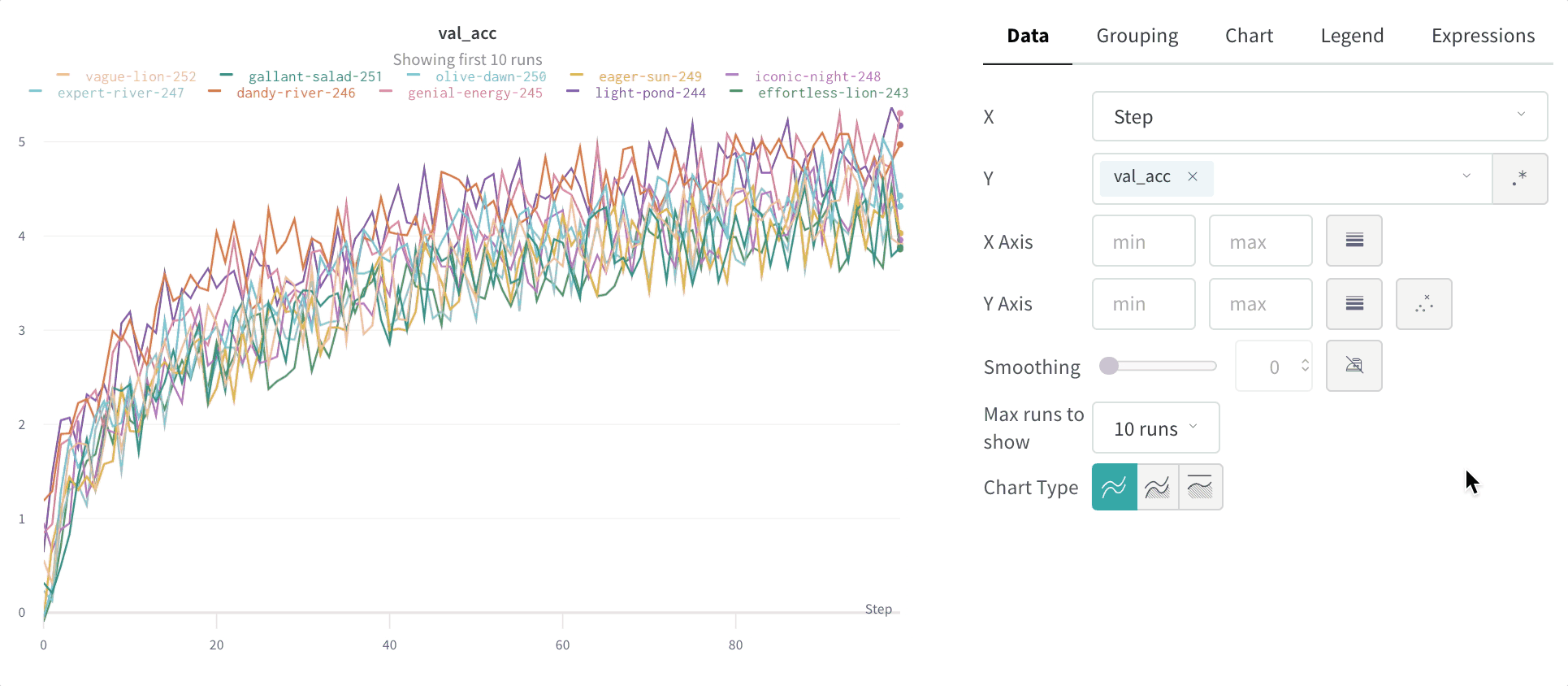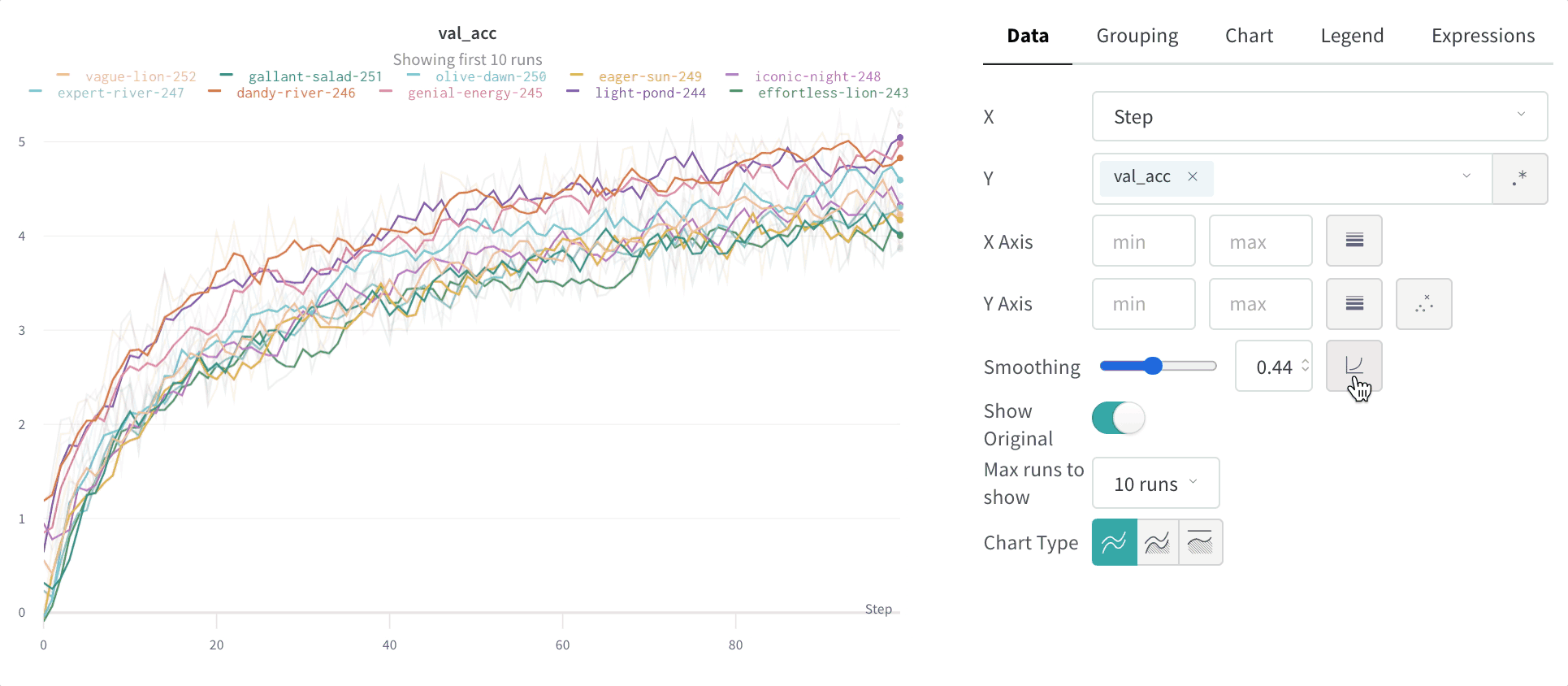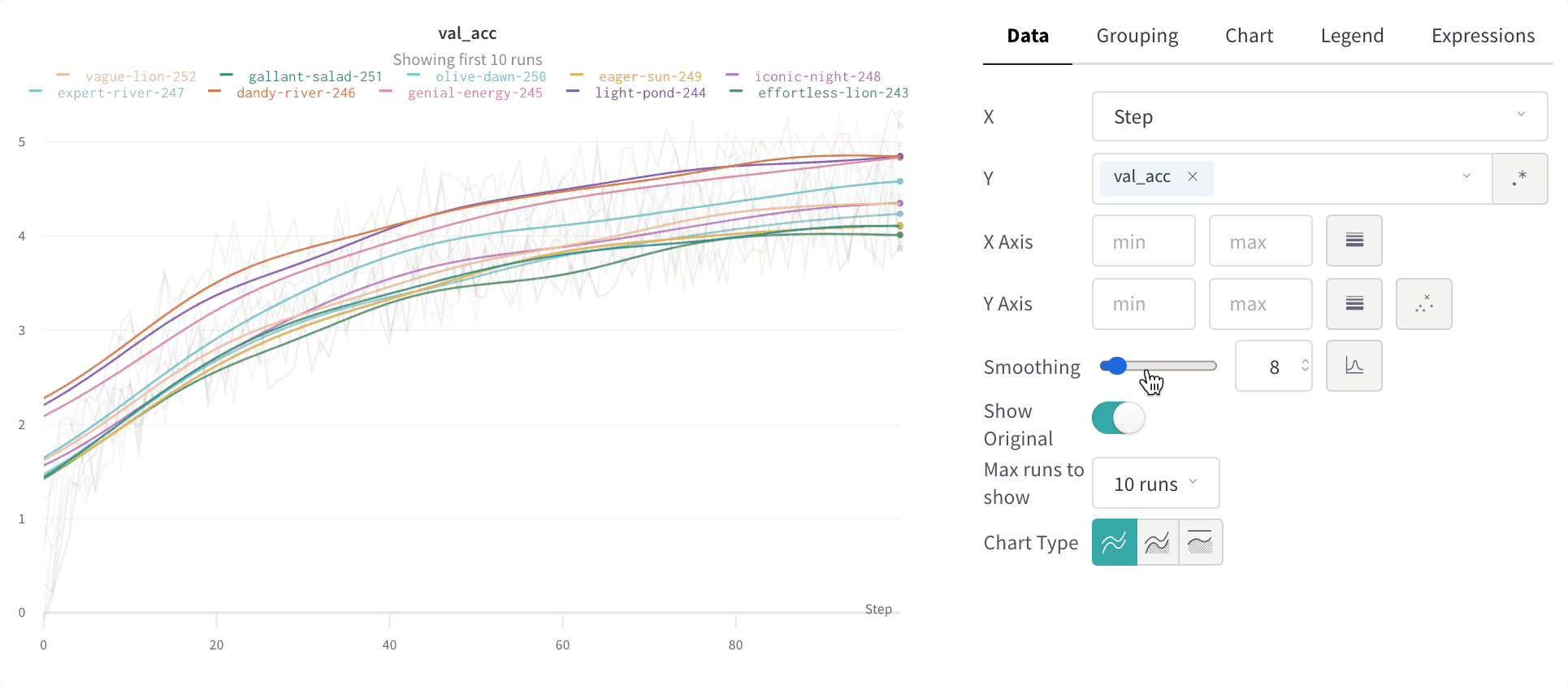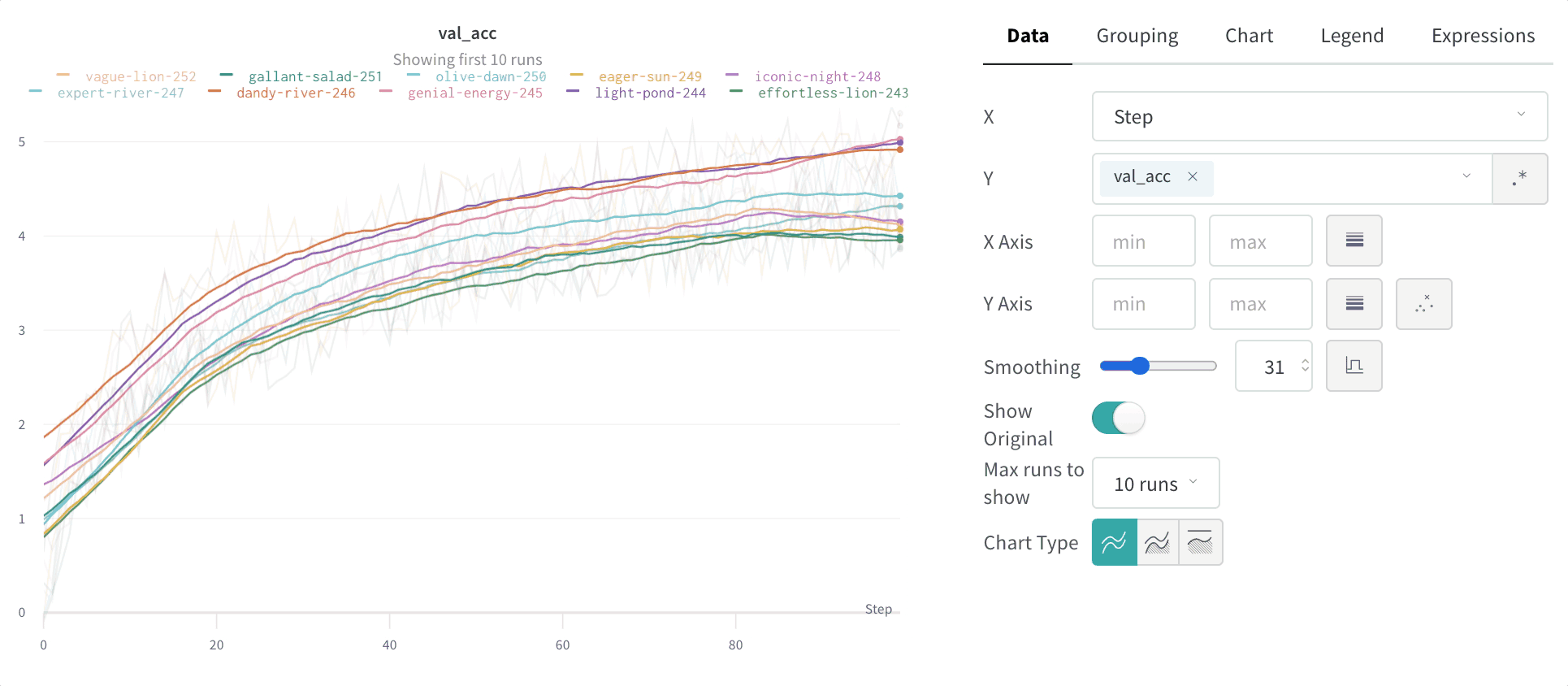
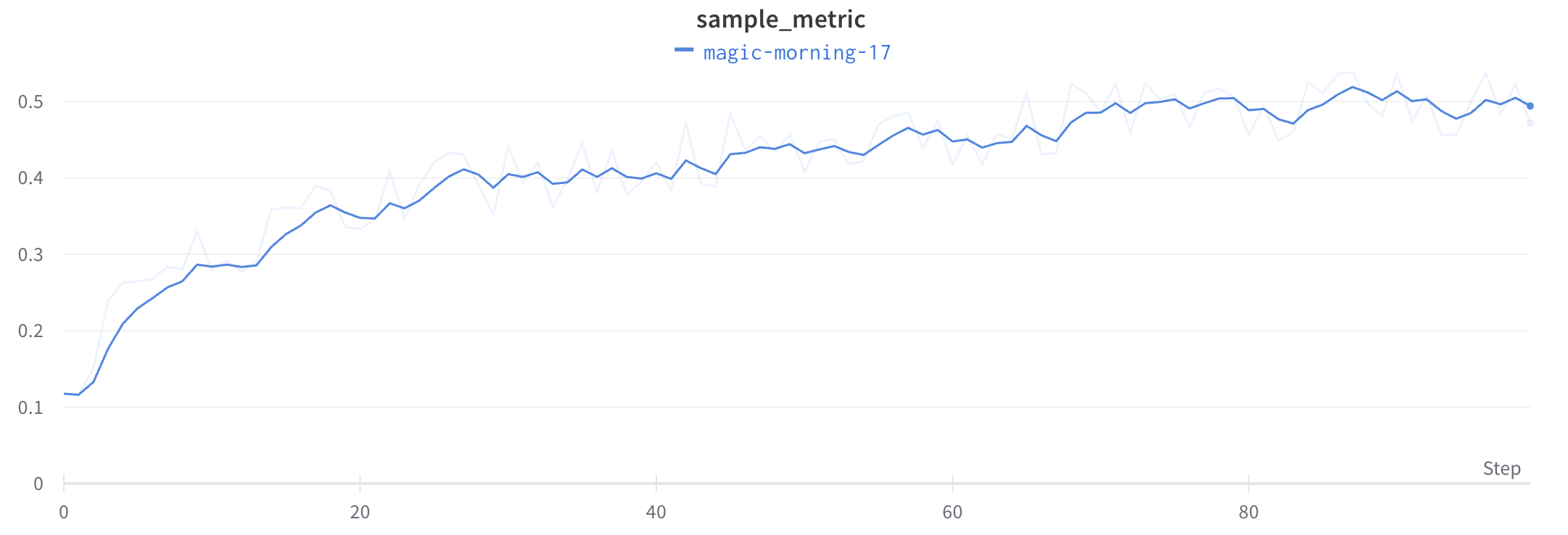
Time Weighted Exponential Moving Average (TWEMA) スムージング (デフォルト)

Time Weighted Exponential Moving Average (TWEMA) スムージングアルゴリズムは、以前のデータポイントの重みを指数関数的に減衰させることで、時系列 データをスムージングする手法です。この手法の詳細については、指数平滑法 を参照してください。範囲は 0 から 1 です。時系列 の初期値が 0 に偏らないよう、バイアス 除去項が追加されています。

TWEMA アルゴリズムは、ライン上のポイントの密度（x軸の単位範囲あたりの y 値の数）を考慮します。これにより、異なる特性を持つ複数のラインを同時に表示する場合でも、一貫したスムージングが可能になります。

以下は、内部でどのように動作するかを示すサンプル コード です：

const smoothingWeight = Math.min(Math.sqrt(smoothingParam || 0), 0.999);
let lastY = yValues.length > 0 ? 0 : NaN;
let debiasWeight = 0;

return yValues.map((yPoint, index) => {
  const prevX = index > 0 ? index - 1 : 0;
  // VIEWPORT_SCALE は結果をチャートの x 軸範囲に合わせてスケーリングします
  const changeInX =
    ((xValues[index] - xValues[prevX]) / rangeOfX) * VIEWPORT_SCALE;
  const smoothingWeightAdj = Math.pow(smoothingWeight, changeInX);

  lastY = lastY * smoothingWeightAdj + yPoint;
  debiasWeight = debiasWeight * smoothingWeightAdj + 1;
  return lastY / debiasWeight;
});

アプリ内 での表示は以下のようになります：

​

Gaussian スムージング

Gaussian スムージング（またはガウスカーネルスムージング）は、ポイントの加重平均を計算します。重みは、スムージング パラメータ として指定された標準偏差を持つガウス分布に対応します。スムージングされた 値 は、各入力 x 値に対して、その前後に発生するポイントに基づいて計算されます。

アプリ内 での表示は以下のようになります：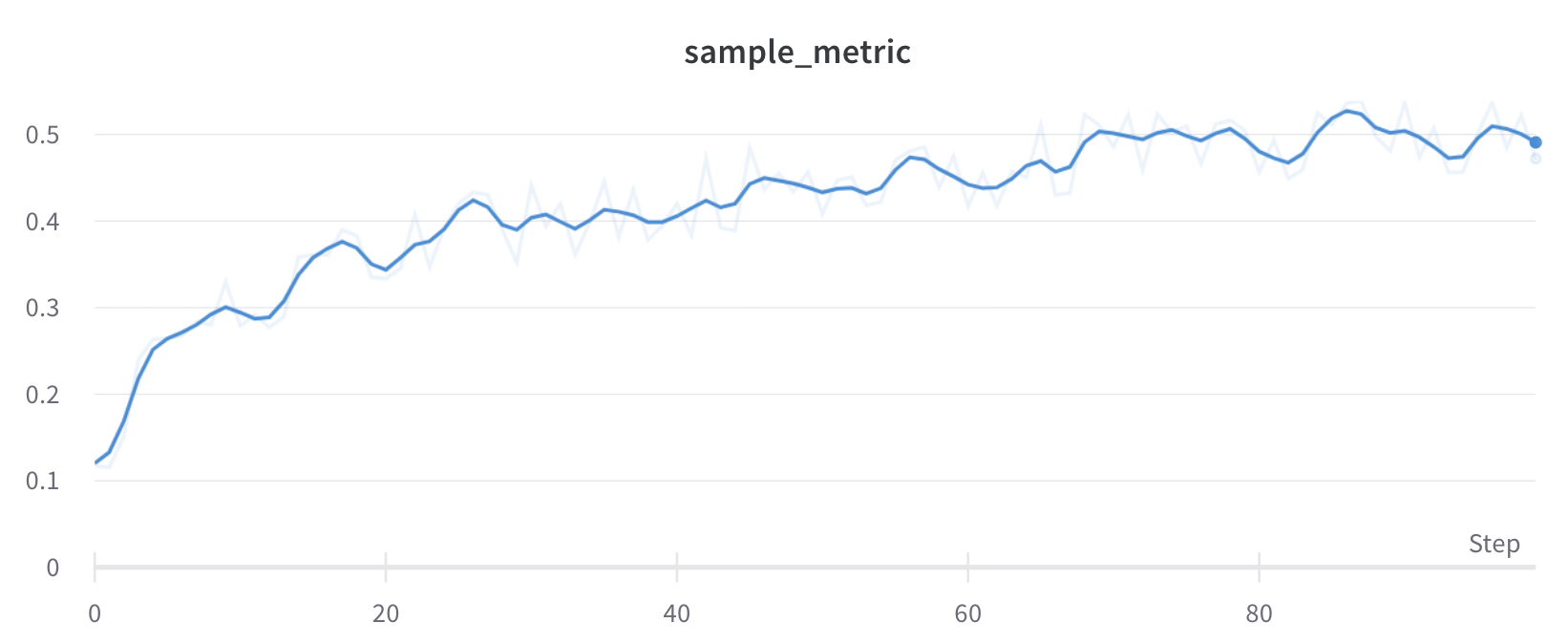

​

Running average スムージング

Running average（移動平均）は、あるポイントを、指定された x 値の前後にあるウィンドウ内のポイントの平均値で置き換えるスムージングアルゴリズムです。詳細は Wikipedia の「Boxcar Filter」 を参照してください。Running average で選択された パラメータ は、移動平均で考慮するポイントの数を Weights and Biases に伝えます。

x 軸上のポイントの間隔が不均等な場合は、代わりに Gaussian スムージングの使用を検討してください。

アプリ内 での表示は以下のようになります：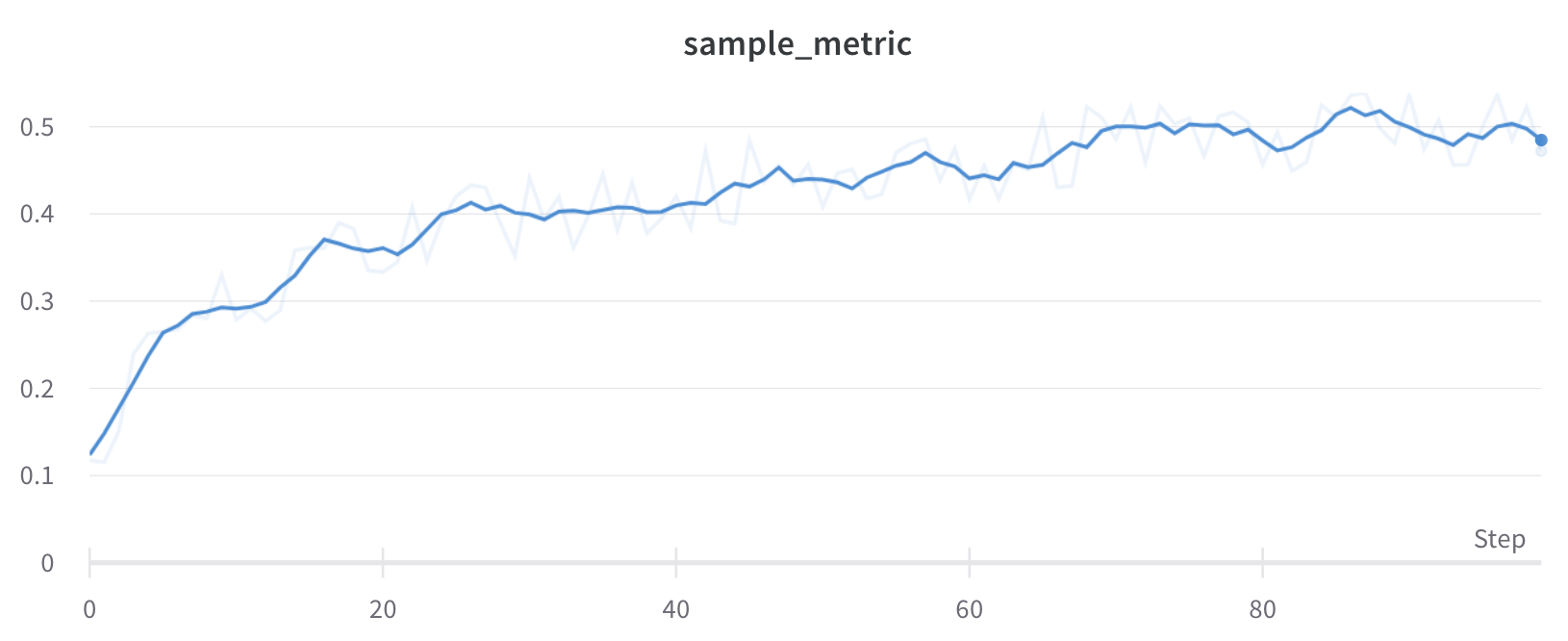

​

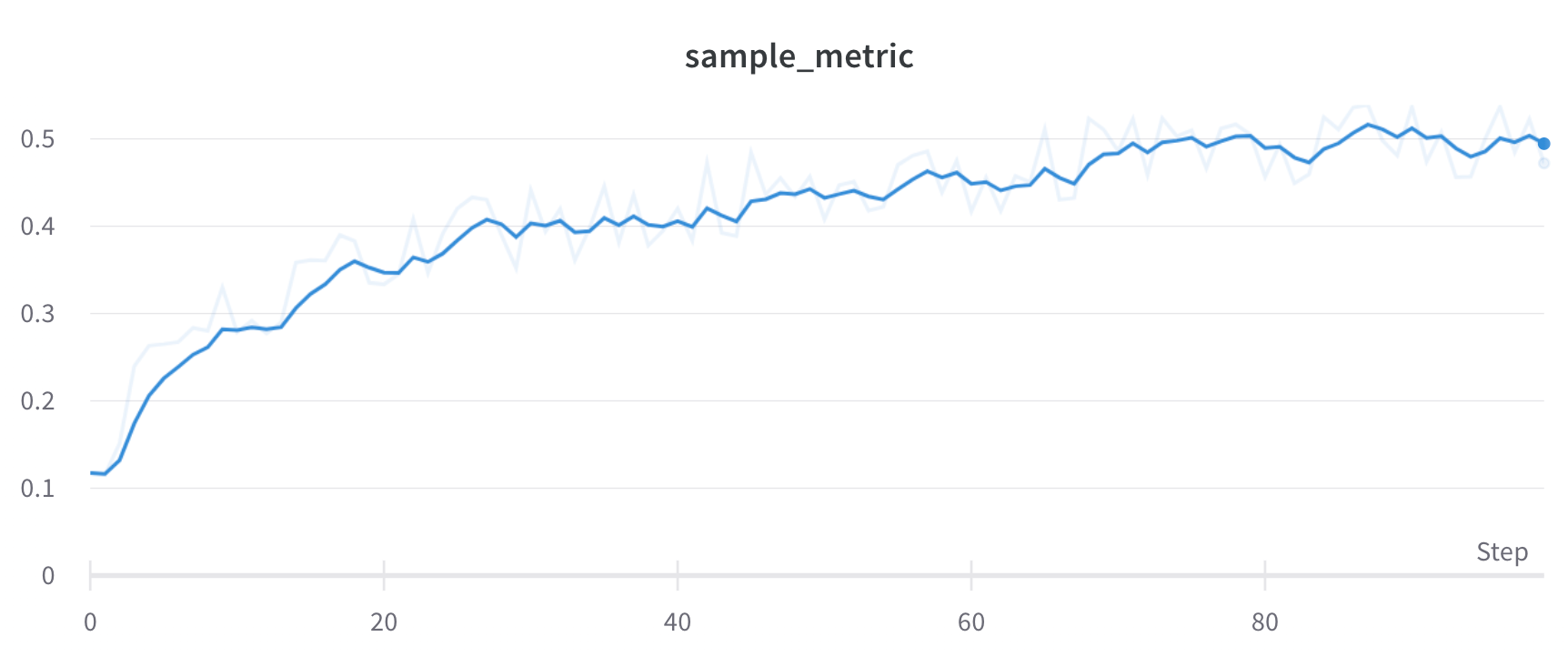
Exponential Moving Average (EMA) スムージング

Exponential Moving Average (EMA) スムージングアルゴリズムは、指数ウィンドウ関数を使用して 時系列 データをスムージングする経験則的な手法です。この手法の詳細については、指数平滑法 を参照してください。範囲は 0 から 1 です。時系列 の初期値が 0 に バイアス されないよう、デバイアス項が追加されています。

多くの場合、EMA スムージングはスムージング前に バケット 化するのではなく、履歴のフルスキャンに適用されます。これにより、より正確なスムージングが得られることがよくあります。

以下のような状況では、代わりに バケット 化の後に EMA スムージングが適用されます：

• サンプリング
• グルーピング
• 式（Expressions）
• 非単調な x 軸
• 時間ベースの x 軸

以下は、内部でどのように動作するかを示すサンプル コード です：

  data.forEach(d => {
    const nextVal = d;
    last = last * smoothingWeight + (1 - smoothingWeight) * nextVal;
    numAccum++;
    debiasWeight = 1.0 - Math.pow(smoothingWeight, numAccum);
    smoothedData.push(last / debiasWeight);

アプリ内 での表示は以下のようになります：

​

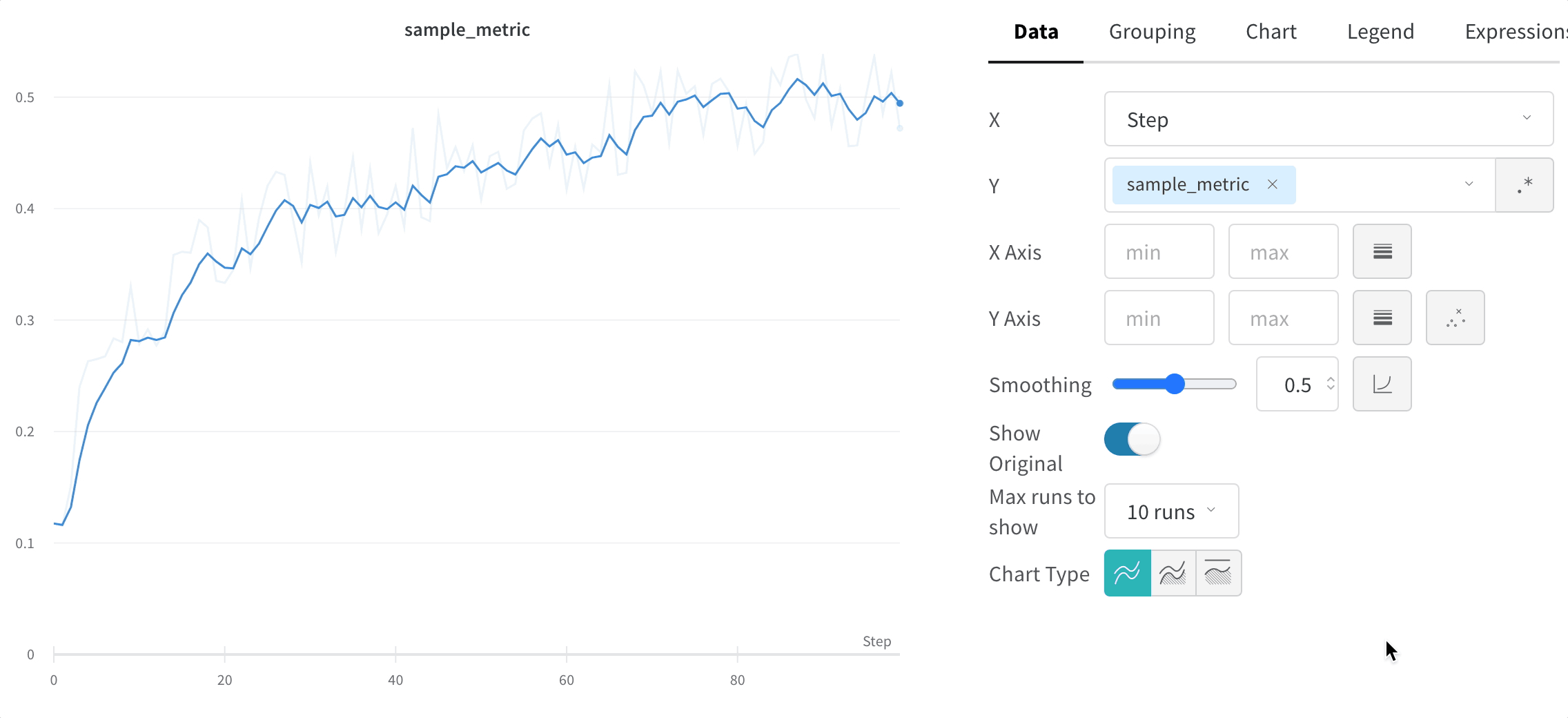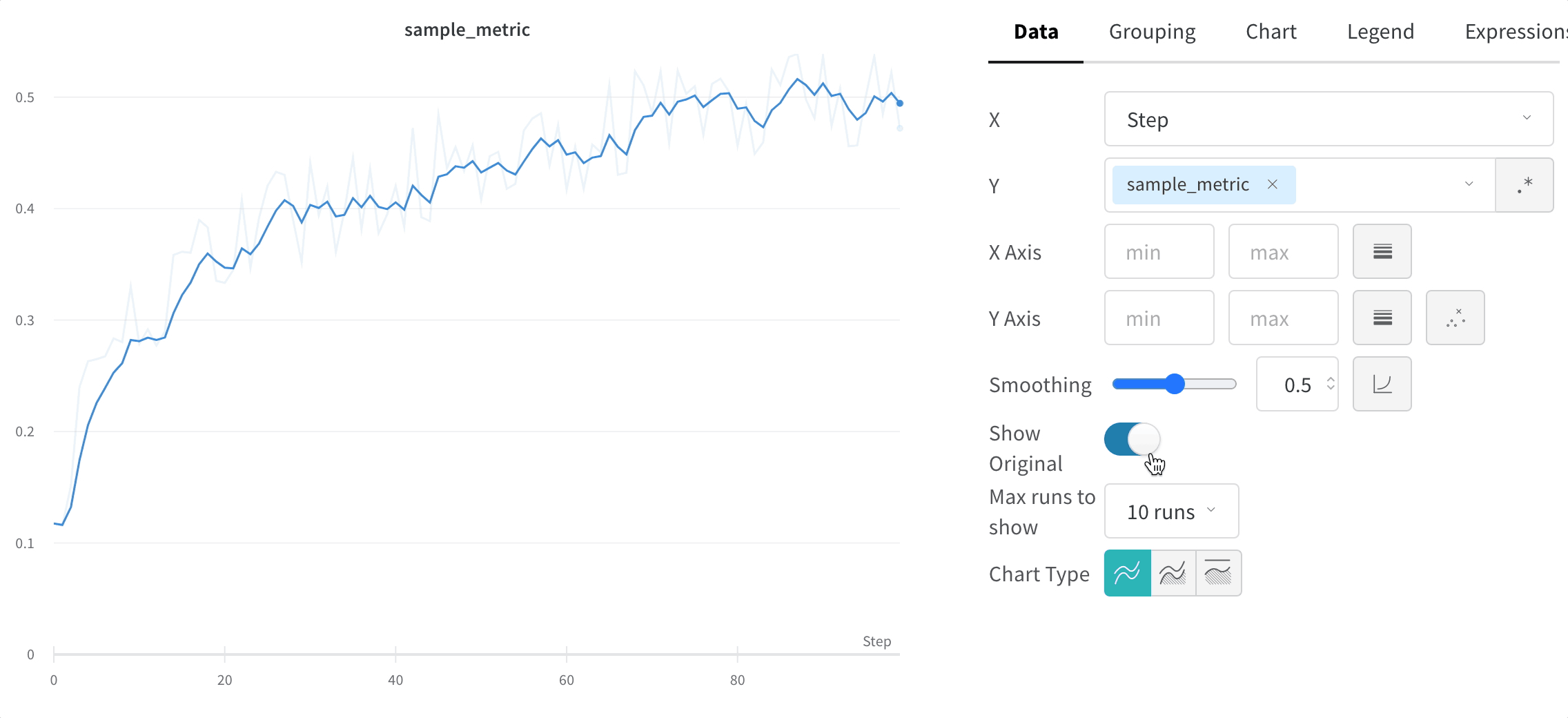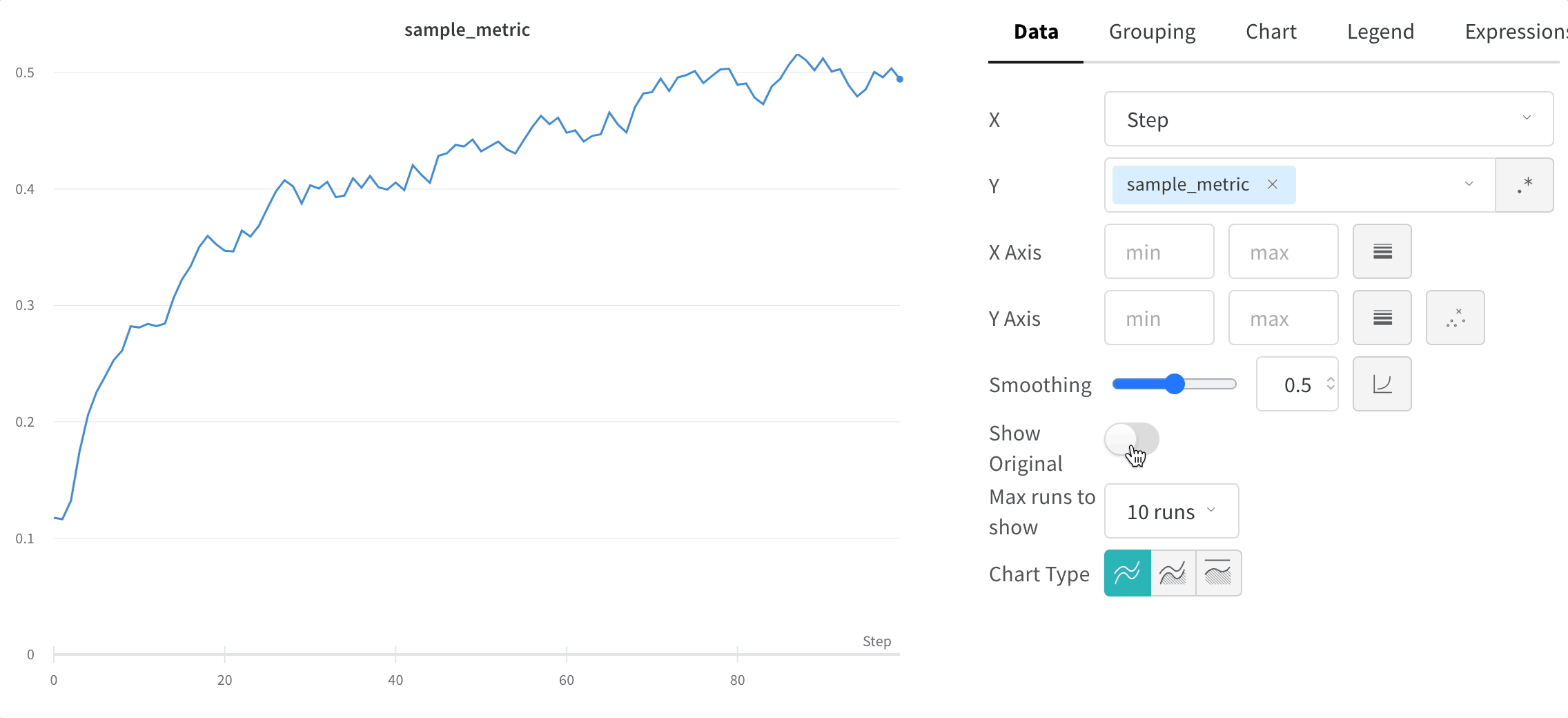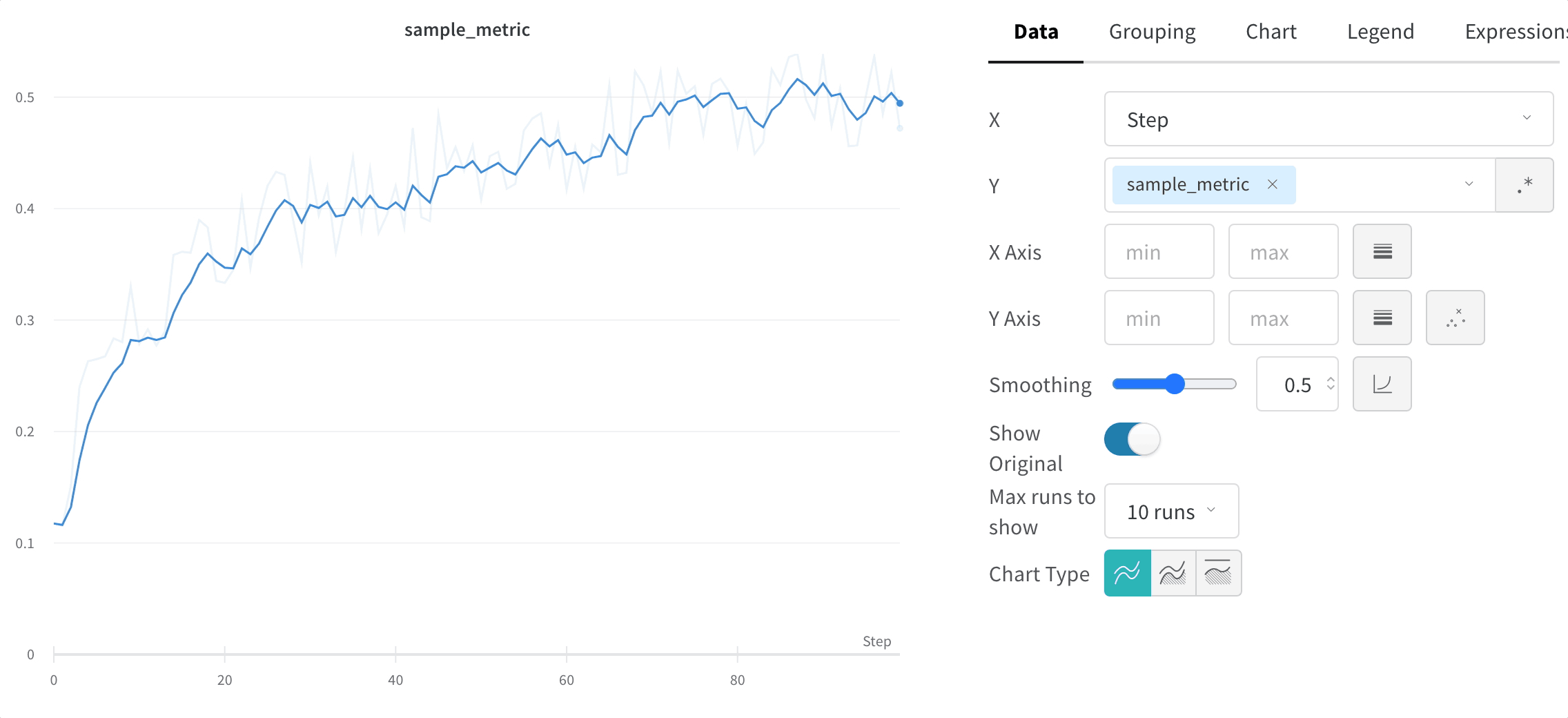
元のデータを非表示にする

デフォルトでは、スムージングされていない元の データ がプロットの背景に薄い線として表示されます。これをオフにするには、Show Original をクリックします。